What Are Graphs?

Definition: Graphs are a fundamental mathematical structure for representing complex systems. At their core, a graph is composed of a set of entities, called nodes (or vertices), and a set of edges that encode relationships between them. Unlike representations that focus solely on individual entities, graphs explicitly model the interactions, dependencies, and structure of a system.

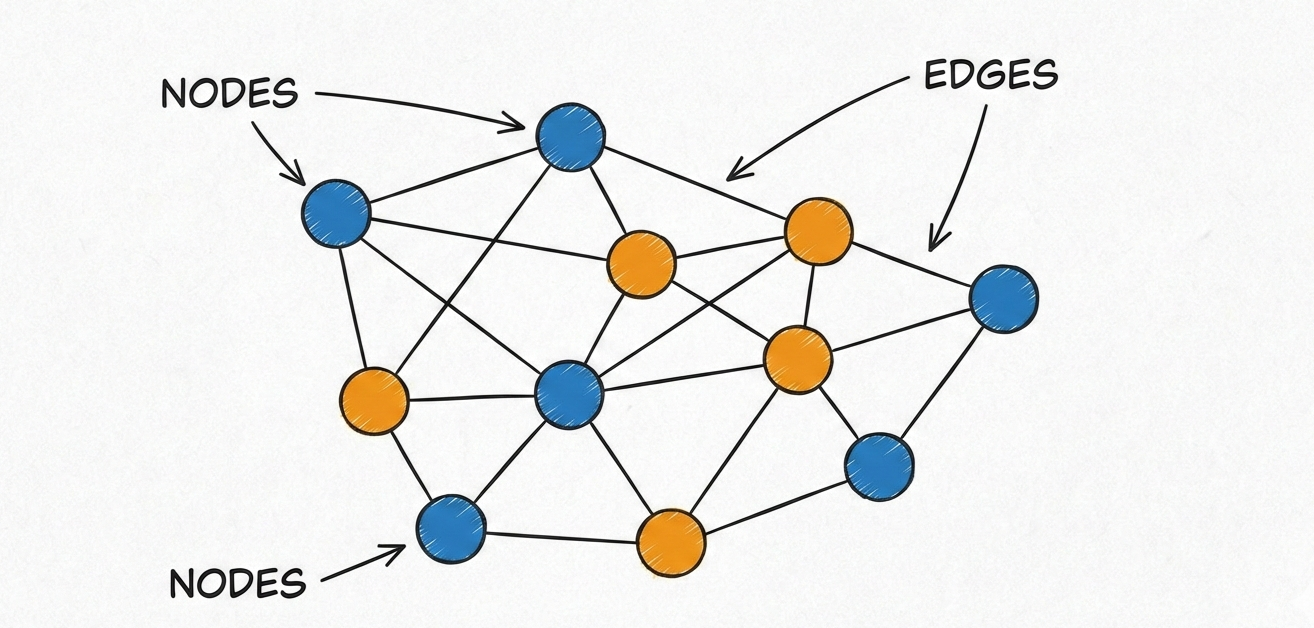
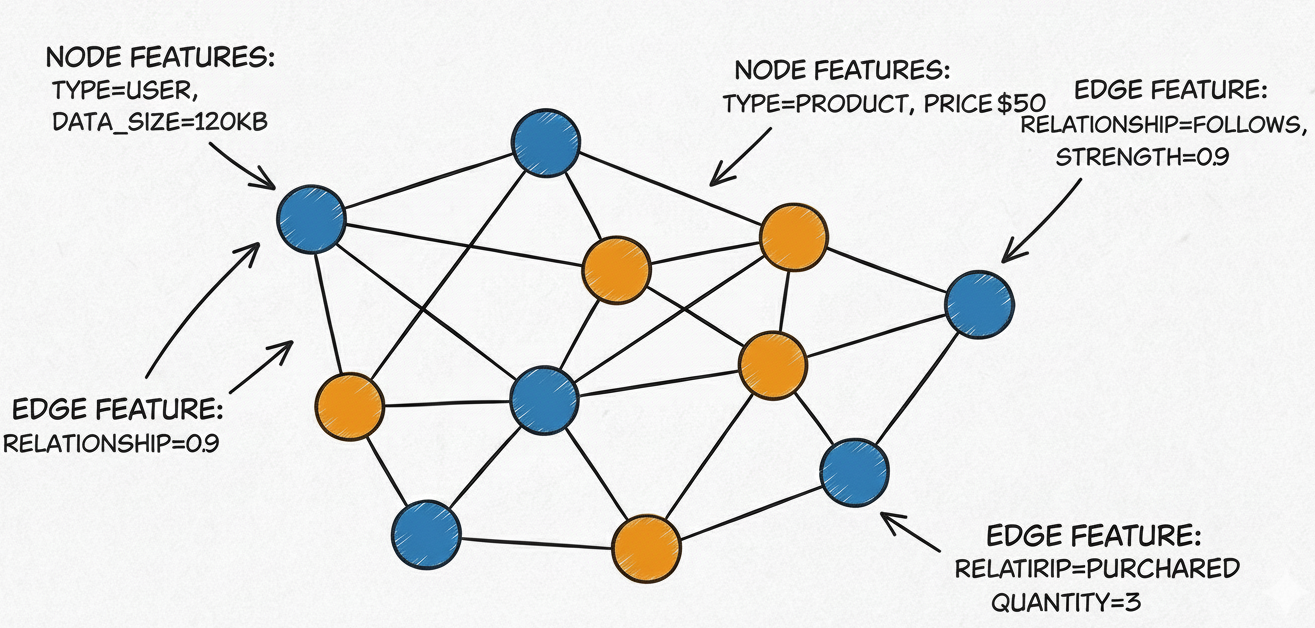
This relational viewpoint, combined with their expressive power, makes graphs a highly versatile tool across many domains.

Examples

• Social networks: Nodes represent individuals, and edges denote relationships such as friendships or interactions.
• Biology: Nodes may correspond to proteins, while edges represent biochemical or functional interactions.

---

Why Graphs?

Unlike tabular data or grid-structured data (e.g., images or text), graphs naturally encode both entities and their relationships. This makes them particularly well suited for domains where connectivity and interdependence are central, including:

• social and communication networks,
• molecular and biological systems,
• knowledge graphs,
• transportation and infrastructure networks.

---

What Is a Graph?

Before applying machine learning techniques to graph-structured data, we first introduce a formal definition.

Formal Definition

A graph is defined as
\begin{equation} G = (V, E), \end{equation} where:

• \((V = \{v_1, v_2, \dots, v_n\})\) is a finite set of nodes (vertices), and
• \((E \subseteq V \times V)\) is a set of edges, representing relationships between nodes.

An edge connecting nodes \((u, v \in V)\) is denoted by \(((u, v) \in E)\).

In this README, we primarily consider simple, undirected graphs, which satisfy:

• At most one edge exists between any pair of nodes.
• Self-loops (edges of the form \((u, u)\)) are not allowed.
• Edges are undirected, meaning: \begin{equation} (u, v) \in E \iff (v, u) \in E. \end{equation}

---

Adjacency Matrix Representation

A common and convenient representation of a graph is the adjacency matrix \begin{equation} A \in \mathbb{R}^{|V| \times |V|}. \end{equation}

To construct the adjacency matrix:

1. Assign each node \((v_i \in V)\) a unique index $$(i \in {1, \dots,

   V

   })$$.

2. Define the matrix entries as: \begin{equation} A_{uv} = \begin{cases} 1, & \text{if } (u, v) \in E,
   0, & \text{otherwise}. \end{cases} \end{equation}

Key properties:

• For undirected graphs, the adjacency matrix is symmetric: \begin{equation} A_{uv} = A_{vu}. \end{equation}
• For directed graphs, symmetry is not required, as edge direction is preserved.

---

📌 Basic Graph Types

Before introducing multi-relational graphs, it is useful to review the most common graph types.

---

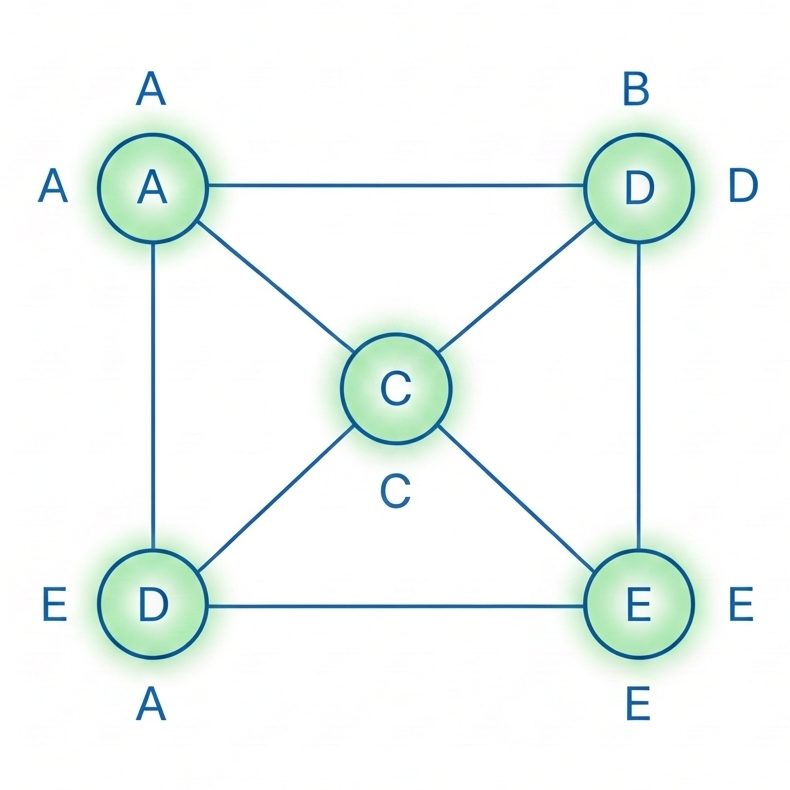
🔹 Undirected Graphs

In undirected graphs, edges have no orientation. The relationship between two nodes is bidirectional, meaning that if node (u) is connected to node (v), then (v) is also connected to (u).

[ (u, v) \in E \iff (v, u) \in E ]

Characteristics:

• No direction associated with edges
• Adjacency matrix is symmetric
• Common in social or physical interaction networks

Example:
Friendship networks, where friendship is mutual.

---

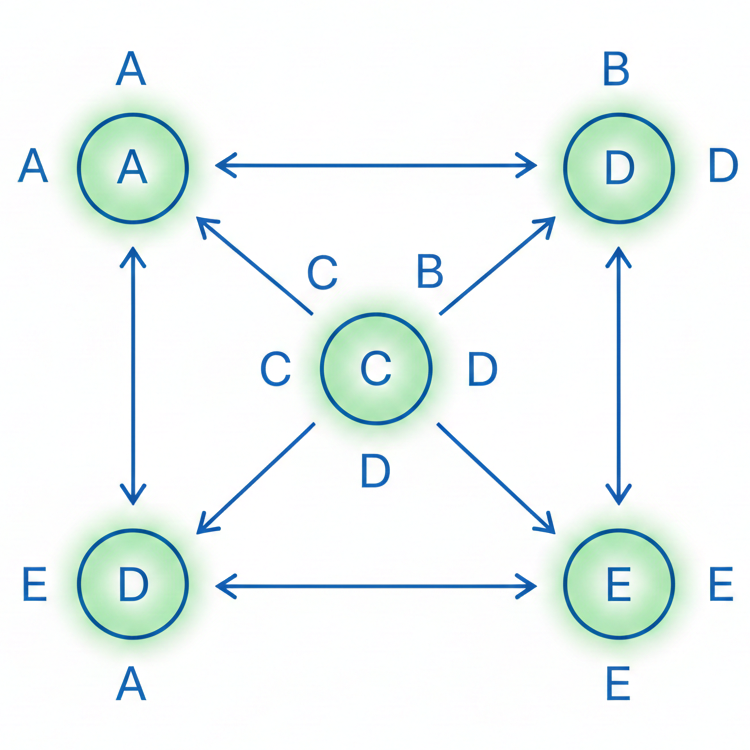
🔹 Directed Graphs

In directed graphs (also called digraphs), edges have a direction. An edge from node (u) to node (v) does not imply the existence of an edge from (v) to (u).

[ (u, v) \in E \;\;\not\Rightarrow\;\; (v, u) \in E ]

Characteristics:

• Edges have direction
• Adjacency matrix is not necessarily symmetric
• Captures asymmetric relationships

Example:
Citation networks, where one paper cites another.

---

🔹 Weighted Graphs

In weighted graphs, each edge is associated with a numerical value (weight) that represents the strength, cost, or capacity of the connection.

\[(u, v, w) \in E,\quad w \in \mathbb{R}\]

Characteristics:

• Edge weights encode quantitative information
• Can be combined with directed or undirected graphs
• Adjacency matrix stores weights instead of binary values

Example:
Road networks, where weights represent distances or travel times.

---

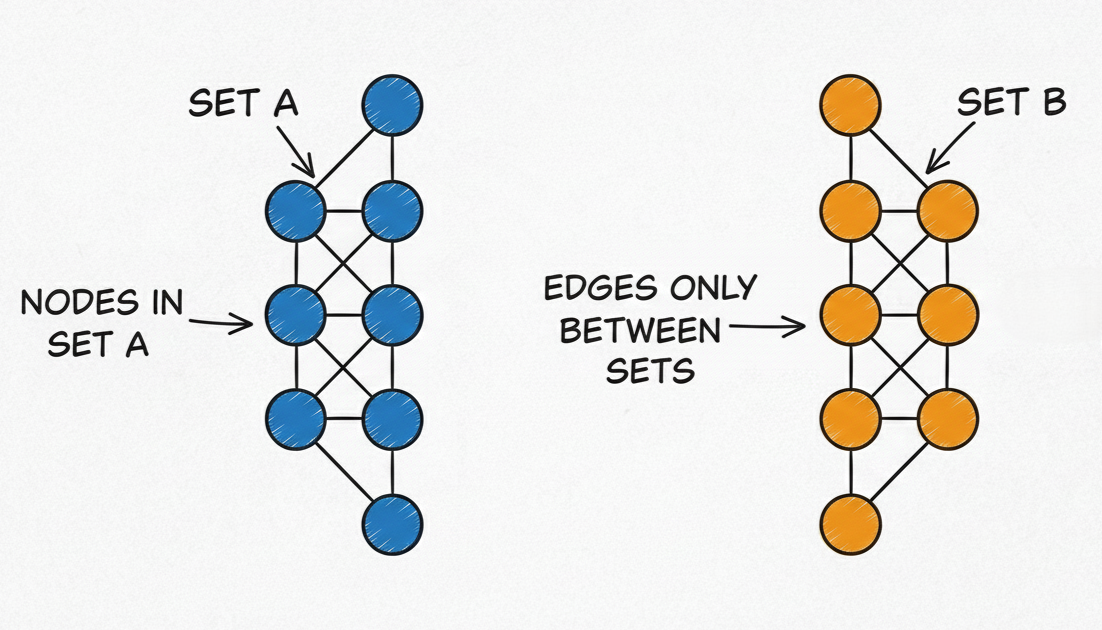
Bipartite Graph

A bipartite graph is a graph whose set of vertices can be divided into two disjoint sets $(V_1)$ and (V_2) such that:

• Every edge connects a vertex in (V_1) to a vertex in (V_2)
• No edge exists between vertices within the same set

Formally, a graph (G = (V, E)) is bipartite if:

\[V = V_1 \cup V_2,\quad V_1 \cap V_2 = \varnothing\]

and for every edge ((u, v) \in E):

\[u \in V_1,\ v \in V_2 \quad \text{or} \quad u \in V_2,\ v \in V_1\]

Key Properties

• Bipartite graphs contain no odd-length cycles
• They are 2-colorable, meaning vertices can be colored using two colors so that no adjacent vertices share the same color
• Commonly used to model relationships between two different types of entities

Examples

• Trees are always bipartite
• Complete bipartite graphs are denoted (K_{m,n}), where every vertex in one set is connected to every vertex in the other set

Applications

• User–item graphs in recommendation systems
• Student–course assignment problems
• Matching problems (e.g., maximum bipartite matching)

Weighted Graphs

In many real-world applications, edges carry additional information in the form of weights, which may represent strength, cost, similarity, or capacity. In this case, the adjacency matrix becomes: \begin{equation} A_{uv} \in \mathbb{R}. \end{equation}

For example, in a protein–protein interaction network, an edge weight may encode the confidence or intensity of interaction between two proteins, rather than a simple binary connection.

Multi-Relational Graphs

Graphs are powerful structures for representing complex systems. Beyond the classical distinction between undirected, directed, and weighted graphs, many real-world problems require modeling multiple types of relationships between nodes. These are known as multi-relational graphs.

---

📌 What Are Multi-Relational Graphs?

In multi-relational graphs, edges are associated with relation types. Instead of representing an edge simply as a pair of nodes ((u, v)), we extend the notation to:

[ (u, \tau, v) \in E ]

where:

• (u, v \in V) are nodes,
• (\tau \in R) is a relation (or edge) type,
• (R) is the set of all relation types.

Each relation type (\tau) can be represented by its own adjacency matrix (A_\tau). Collectively, the entire graph can be represented as an adjacency tensor:

[ A \in \mathbb{R}^{|V| \times |R| \times |V|} ]

This representation allows us to model rich relational structures, such as different types of interactions between the same entities.

---

🧬 Example: Drug–Drug Interaction Graphs

In biomedical applications, nodes may represent drugs, and edges may represent different side effects that occur when two drugs are taken together. Each side effect corresponds to a different relation type, making this a natural example of a multi-relational graph.

---

🧩 Types of Multi-Relational Graphs

Two important subclasses of multi-relational graphs are heterogeneous graphs and multiplex graphs.

---

🔹 Heterogeneous Graphs

In heterogeneous graphs, nodes themselves have types. The node set is partitioned into disjoint subsets:

[ V = V_1 \cup V_2 \cup \dots \cup V_k \quad \text{where } V_i \cap V_j = \varnothing \text{ for } i \neq j ]

Edges are constrained by node types. Typically, only certain node-type combinations are allowed for a given relation type:

[ (u, \tau_i, v) \in E \Rightarrow u \in V_j,\; v \in V_k ]

Example: Biomedical Heterogeneous Graph

• Node types: proteins, drugs, diseases
• Edge types:
  • treats: drug → disease
  • polypharmacy side-effect: drug ↔ drug

Multipartite Graphs

A special case of heterogeneous graphs where edges only connect nodes of different types:

[ (u, \tau_i, v) \in E \Rightarrow u \in V_j,\; v \in V_k,\; j \neq k ]

---

🔹 Multiplex Graphs

In multiplex graphs, the graph is decomposed into multiple layers, each corresponding to a different relation type.

Key assumptions:

• Every node exists in every layer
• Each layer represents one intra-layer relation
• Inter-layer edges may connect the same node across layers

Example: Transportation Network

• Nodes: cities
• Layers:
  • Air transportation
  • Train transportation
• Intra-layer edges: connections between cities using the same mode
• Inter-layer edges: switching transportation modes within the same city

Multiplex graphs are particularly useful for modeling multi-modal systems where entities participate simultaneously in multiple types of interactions.

---